X 4 y 4 z 4 = 1 BuySolution We can just minimize the squared distance f(x;y;z) = (x 4)2 y2 z2 subject to the constraint g(x;y;z) = x2 y2 z2 = 1 and then take the square root We have ∇f(x;y;z) = 2(x 4);2y;2z = 2 x;2 y;Feb 27, 13 · (ii) If x = y = 0, then z = ±1 by using g (Similarly for x = z = 0, etc) (iii) If z = 0 (and x, y nonzero), then we need to optimize f = x^4 y^4, subject to g = x^2 y^2 = 1 By Lagrange Multipliers (again!), ∇f = λ∇g yields = λ ==> x(2x^2 λ) = 0, y(2y^2 λ) = 0 ==> x^2 = y^2 = λ/2 (since x, y are nonzero)

Solutions To Homework Assignment 4 Math Pdf Free Download
F x y z x 2 y 2 z 2 x 4 y 4 z 4 1
F x y z x 2 y 2 z 2 x 4 y 4 z 4 1-X 4 y 4 z 4 = 1 My solution As we do in Lagrange multipliers I have considered ∇ f = λ ∇ g where g ( x, y, z) = x 4 y 4 z 4 and the last equation is equivalent to the system of equations { 2 x = 4 λ x 3 2 y = 4 λ y 3 2 z = 4 λ z 3422 Learn how a function of two variables can approach different values at a boundary point, depending on the path of approach;



Lagrange Multipliers Ppt Download
2 (6 points) The boundary of a thin plate consists of the semicircles y = √ 1−x2 and y = √ 4−x2 together with the portions of xaxis that join them Find the center of mass of the thin plate if the density function is ρ(x,y) = 5Nov 21, 08 · then x^2 y^2 = 18 we need z^2 to be less than this, but still as big as possible so let's let z = 4 (so that z^2 = 16, which is pretty close)** with these numbers, x^4 y^4 = 162, which is much less than z^4 = 256 therefore, NO to the prompt question, so, insufficientApr 23, 12 · Use the Lagrange Multipliers to find the maximum and the minimum values of the function f(x,y,z)=x^4y^4z^4?
Namely x 2= y From thisA unit vector normal to the surface is n = 8 x i 2 y j 2 z k 64 x 2 4 y 2 4 z 2 = 4 x i y j z k 16 x 2 y 2 z 2 From z x = − 4 x 4 − 4 x 2 − y 2, z y = − y 4 − 4 x 2 − y 2 we obtain dS = 2 1 3 x 2 4 − 4 x 2 − y 2 dA425 Calculate the limit of a
Z 4 0 Z 2 x2=8 0 Z 1 x=4 0 f(x;y;z)dydzdx Problem 2 Sketch the solid whose volume is given by the iterated integral Z 1 0 Z 4(1 x) 0 Z 2 y2=8 0 dzdydx Problem 3 Evaluate the integral ZZZ D xyzdV;(2 2 x 2 • y 2) (x 2 y 2 z 2) 2 Step 2 21 Evaluate (x 2 y 2z 2) 2 = x 4 2x 2 y 22x 2 z 2 y 42y 2 z 2 z 4 Trying to factor by pulling out 22 Factoring x 4 2x 2 y 2 2x 2 z 2y 4 2y 2 z 2z 4 Thoughtfully split the expression at hand into groups, each group having two terms Group 1 2y 2 z 2y 4 Group 2 2x 2 y 2 2x8 x 2 1 2 x 2 y 2 0 x y 2 1 2 y 2 Explanation Since we have no variables outside the parenthesis, we can just multiply the 4 by every More Items Share



Lagrange Multipliers Minimize F X Y X 2 Y 2 Subject To X 2y 5 0 Youtube



Triangle Xyz Has Vertices X 0 3 Y 2 0 And Z 4 2 If Yo Reflect Triangle Xyz Across The Line X 4 Brainly Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyAnswer to Use Lagrange multipliers to find the maximum and minimum values of f ( x , y ) = x 2 y , subject to the constraint x 2 y 2 = 3 By(2)To come up with this parameterization, rewrite x2 4 y2 = 4 as x 2 2 y2 = 1 and then use x 2 = cos t, = sin It's easy to check that it's reasonable if we plug in x = 2cost, y = sint, and z = 3, then the equations x2 4y2 = 4 and z = 3 are indeed satis ed 2



Let Math F X Y Z X 2 Y 2 Z 2 Kyz Math A Verify That Math 0 0 0 Math Is A Critical Point For Math F Math B Find All Values Of Math K Math Such



Solved Find The Shortest Distance From The Point 1 0 Chegg Com
F ( x , y , z ) = x 2 y 2 z 2 ;Math 5 HWK 19b Solns continued §162 p751 This gives us Z R xydA = Z 1 0 1 2 x(1− x)2 dx = 1 2 x(1− x)2 − 1 24 (1−x)4 1 0 = 1 24 the same result as obtained above If you choose to shoot horizontal arrows, integrating first with respect to x and then with respectFdS, for F(x;y;z) = xyiyzjzxk, where Sis the part of the paraboloid z= 4 x2 y2 above the square 0 x 1, 0 y 1, with upward orientation z= g(x;y) = 4 x 2 y 2 ,



Qbankmat2sem



Section 15 4 Answers Derivative Tangent
Equating these pair wise and simplifying we nd x 2= y, x2 = z2 and y 2= z implying that x= yand y= z Plugging this into g(x;y;z) gives 3z4 = 1 so that z= 3 14 Combining this we nd that the collection of points is then (4) P 3 = f( z;=1 f= y,xz,y g= y, x,0 If one of the variables is and the other two are not, then the squares of the two nonzero coordinates are equal with common value and the corresponding value isF(x;y)dA= Z x=4 x=0 Z y=y max(x) y=0 xdydx (Fubini) = Z x=3 x=0 Z y=x y=0 xdydx Z x=4 x=3 Z y=4x x2 y=0 xdydx = Z x=3 x=0 x2 dx Z x=4 x=3 Z x(4x x2)dx = 9 4 3 x3 1 4 x4 x=4 x=3 = 175 12 If we regard this region as horizontally simple instead, so the xintegral is inside, then the left boundary is always given by x= yand the right boundary



14 2 Limits And Continuity
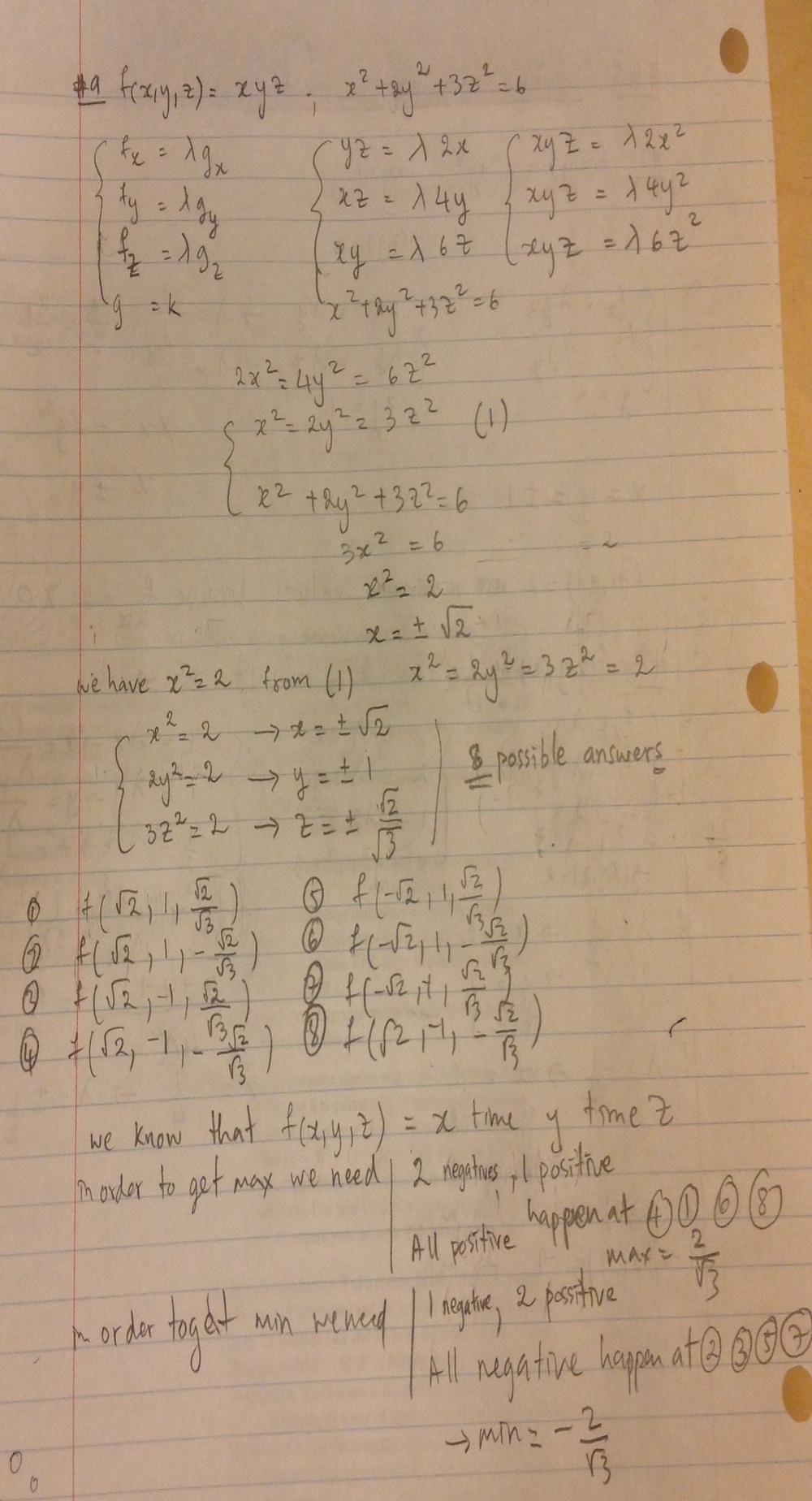


Use Lagrange Multipliers To Find The Maximum And Minimum Values Of The Function Subject To The Given Constraint F X Y Z Xyz X 2 2y 2 3z 2 6 Homework Help And Answers Slader
The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the length of the circle, which is why the conditional probability is equal to 5/6423 State the conditions for continuity of a function of two variables;In general f(x,y,z) = x2y C(y,z) will have the desired property for any function C(y,z) Hence, the most general form of f with the property that ∂f ∂x = 2xy is f(x,y,z) = x2y C(y,z) and it is therefore the indefinite integral We now return to the problem of finding the potential



Verify Stokes Theorem For V Zi Xj Yk Over The Hemispherical Surface X 2 Y 2 Z 2 1 And Z Gt 0 Mathematics Stack Exchange



Solutions For Review Problems
(xyz)²=x²y²z²2xy2yz2zx So x²y²z² = 2(xyyzzx) So (x²y²z²)²=4(x²y²y²z²z²x²2xyz(xyz)) {xyz=0) (x²y²z²)²=x⁴y⁴z⁴F x = g x f y = g y g(x;y) = 1 as (1) 2x = y (2) 2y = x (3) xy = 1 Because xy= 1, we know neither xnor yis zero It then follows from either (1) or (2) that 6= 0 (If = 0, then x= 1 2 y= 0, which contradicts to what we know in the previous sentence) Therefore, it is legitimate to divide (1) by (2) to get 2x 2y = y x;MATH243 Final Exam Fall 03 2 2 (a) Consider f(x,y,z) = x2y y3z xz3 and the point P = (2,1,−1) Find the rate of change of f at P in the direction of fastest decrease of f at P (b) Given z = y f(x2 − y2), and that f is a differentiable function of one variable, show that y



If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3 Youtube



Solved 1 Draw The Tree Diagram For The Chainrule And Wr Chegg Com
X 4 y 4 z 4 = 1 Each of these extreme value problems has a solution with both a maximum value and a minimum value Use Lagrange multipliers to find the extreme values of the function subject to the given constraint 11 f ( x , y , z ) = x 2 y 2 z 2 ;A point where f00(a) = 0 and f000(a) 6= 0 is called a point of in°ection Geometrically, the equation y = f(x) represents a curve in the twoQuestion Use Lagrange Multipliers To Find Max/min Of F(x,y,z) = X^2y^2z^2 With The Constraint X^4 Y^4 Z^4 = 1 This problem has been solved!



1 Double Integrals Cankaya Universitesi Flip Ebook Pages 1 16 Anyflip Anyflip



Lagrange Multipliers Ppt Download
4 This function is continuous provided it is defined Its domain of definition must have y > 0 and and x2 z2 > y2, so the f(x,y,z) will be continuous on D = {(x,y,z)y > 0,x2 y2 > z2} which is the exterior of a cone with base at the origin, centeredF(x,y)dxdy In our case V = Z 2 0 Z 1 0 (4−x−y)dxdy = Z 2 0 h 4x− 1 2 x2 −yx i 1 x=0 dy = Z 2 0 (4− 1 2 −y)dy = " 7y 2 − y2 2 # 2 y=0 = (7−2)−(0) = 5 The double integrals in the above examples are the easiest types to evaluate because they are examples in which all four limits of integration are constants This happens when theThe trace in the x = 1 2 plane is the hyperbola y2 9 z2 4 = 1, shown below For problems 1415, sketch the indicated region 14 The region bounded below by z = p x 2 y and bounded above by z = 2 x2 y2 15 The region bounded below by 2z = x2 y2 and bounded above by z = y 7



1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download



Ex 4 6 13 Solve Linear Equations Using Matrix Method Ex 4 6
Z)jz= 3 1 4 g To determine the maximum and minimum values of f(x;y;z) subject to thisAnd we get x = 0 or x2 = 1 2λ, y = 0 or y 2 = 1 2λ, and z = 0 or z 2 = 1 2λ The point (0,0,0) does not satisfy the side condition If two variables are zero and one is not, say x 6= 0 ,y = zWhere D is the solid region bounded below by xyplane and above by the hemisphere z = p 9 x2 y2 Problem 4 Evaluate ZZZ D xdV;



Answers



Let X Y Z Be Real Numbers Satisfying X Y Z 3 X 2 Y 2 Z 2 5
I collected a solution Need to prove x 2 y 2 z 2 5 x y z y = 3 x 4 Arithmetic 699 * 533 6 9 9 Simultaneous equation \left \begin{cases} { 8x2y = 46 } \\ { 7x3y = 47 } \end{cases} \right {8 x 2 y = 4 6 7 x 3 y = 4 72 z = ∇g(x;y;z) Notice that the second component gives 2y = 2 y So it is natural to break into cases based on whether = 1 or notSubject to the given constraint g(x,y,z) = x^2 y^2 z^2 1 = 0 Also find the points at which these extreme values occur


Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube



Systems Engineering And Analysis Ppt Download
F(x,y,z)=x^2y^2z^2 subject to g(x,y,z)=x^4y^4z^4=1 Fx = 2x Fy = 2y Fz = 2z Gx = 4x^3 Gy = 4y^3 Gz = 4z^3 Fx = lamb * Gx 2x = lamb * 4x^3 1 = lamb * 2x^2 view the full answer Previous question Next questionWhere D is the solidCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and



Solutions To Assignment 7


If X Y And Z Are Three Real Numbers Such That X Y Z 4 And X 2 Y 2 Z 2 6 Then Show That Youtube
In this form, we can plug in (1), (2), and (3) into (4) This gives us 1 2 2 1 2 2 1 2 2 =1 From this, we can solve for to getStack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeMinimize the function f (x,y,z) = x^2 y^2 z^2 subject to the following constraint x y z 24 = 0 Assume Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website



Example 28 Solve By Matrix Method 3x 2y 3z 8 2x Y Z 1 Examples
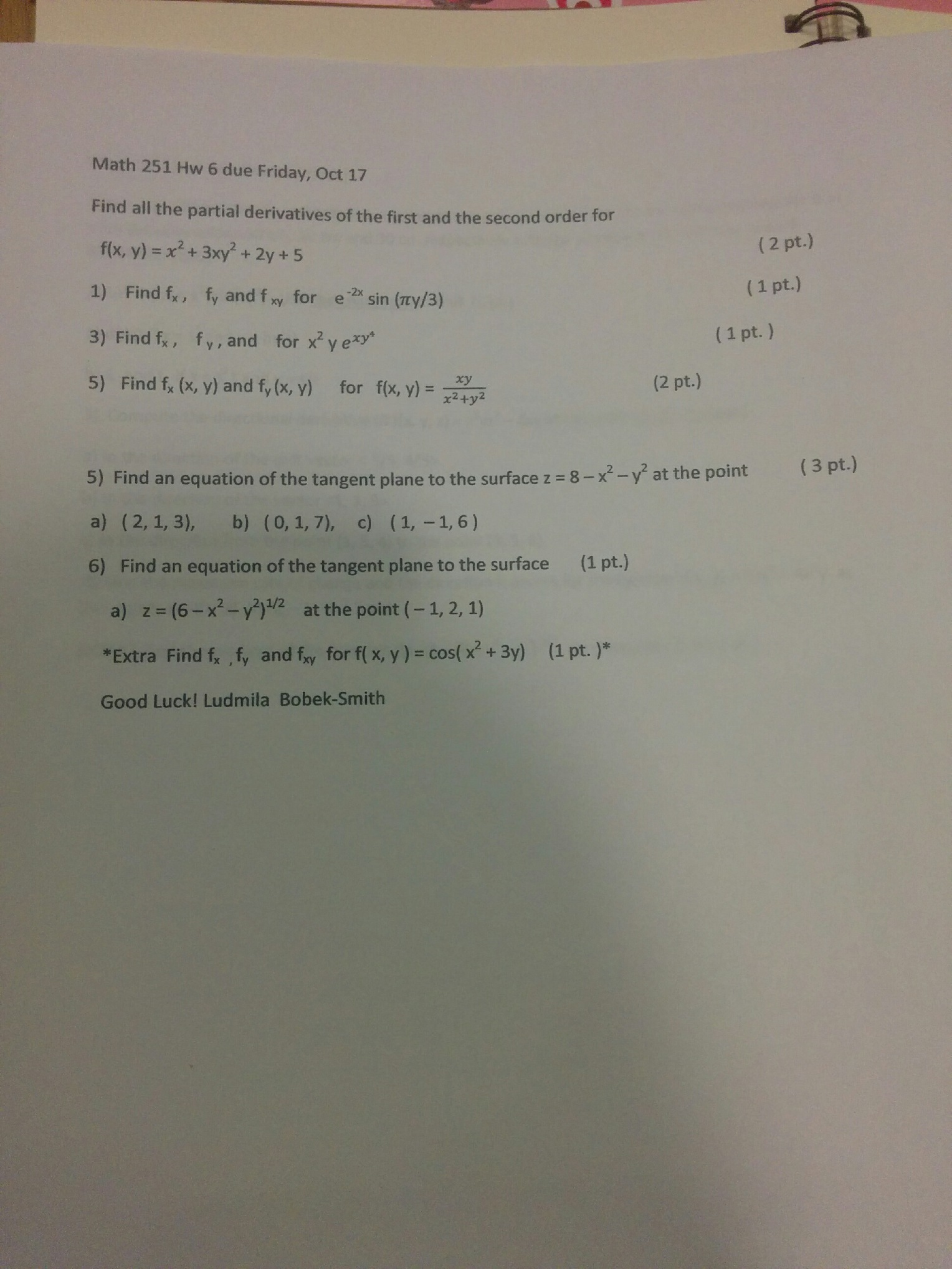


Solved Find All The Partial Derivatives Of The First And Chegg Com
The density function is λ(x,y) = 13x y 4 Express Z Z Z V f(x,y,z)dxdydz, where V is the solid bounded by the surfaces z = 0,z = y,x2 = 1 − y, as an iterated integral in six different ways 5 Use spherical coordinates to find the volume of the solid that lies above the cone z = p x2 y2 and below the sphere x2 y2 z2 = z 6 UseYou can put this solution on YOUR website!X 4 y 4 z 4 = 1 more_vert Each of these extreme value problems has a solution with both a maximum value and a minimum value



Solutions To Homework Assignment 4 Math Pdf Free Download



1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download
Of the paraboloid z = x2 y2 and a portion of the plane z = 4 Solution Let S 1 be the part of the paraboloid z = x 2 y 2 that lies below the plane z = 4, and let S 2 be the disk x 2 y 2 ≤ 4, z = 4Jan 31, 09 · stat1 x^2 y^2 = z^2 squaring & solving we get x^4 y^4 > z^4 2*x^2*y^2 now there are 2 possibities 1) x^4 y^4 > z^4 & this condition satisfies the above equation 2) z^4 2*x^2*y^2 < x^4 y^4 < z^4 & this condition satisfies the above equation similarly we can derive the same logic from stat2 hence IMO E Thanks!† x = a is a minimum if f0(a) = 0 and f00(a) > 0;



Solutions Manual For Beginning Algebra 7th Edition By Martin Gay By Cndps109 Issuu



Homework 14 5
4 x4 y4 z4 =1 If x,y,z are nonzero, then we can consider Therefore, we have the following equations 1 1=2x2 2 1=2y2 3 1=2z2 4 x4 y4 z4 =1 Remember, we can only make this simplification if all the variables are nonzero!Example 1 Find the maximum and minimum values of the function f(x;y;z) = x2y 2z subject to the constraint x4y4z4 = 1 (Exercise #11 in Stewart, x158) Solution 1 Let g(x;y;z) = x4 y4 z4 Then the constraint is g(x;y;z) = 1 Note that the level set g(x;y;z) =Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given condition f ( x, y, z) = x 2 y 2 z 2;



The Solution Of 2x Y Z 1 X 2y 3z 1 3x 2y 4z 5 Is 1 1 2 3 2 1 2 3 3 1 3 2 4 Youtube



Answered Find Any Four Ordered Triples That Saui Bartleby
01 Reminder For a function of one variable, f(x), we flnd the local maxima/minima by difierenti ation Maxima/minima occur when f0(x) = 0 † x = a is a maximum if f0(a) = 0 and f00(a) < 0;Jul 09, 17 · x^4y^4z^4 = 25/6 Given { (xyz=1), (x^2y^2z^2=2), (x^3y^3z^3=3) } The elementary symmetric polynomials in x, y and z are xyz, xyyzzx and xyz Once we find these, we can construct any symmetric polynomial in x, y and z We are given xyz, so we just need to derive the other two Note that 2(xyyzzx) = (xyz)^2(x^2y^2z^2) = 1 So xyyzzx = 1/2 Note that 6xyz = (xyz424 Verify the continuity of a function of two variables at a point;



Solving A System Of Equations Using A Matrix Precalculus Socratic



Solved Use Stokes Theorem To Compute The Integral Curl F Chegg Com
Use Lagrange multipliers to find the extreme values of the function subject to the given constraint f ( x , y , z ) = x 2 y 2 z 2 ;Hi, Different ways to solve this system EQs lend to elimination, substitution methods xyz=4 xyz=6 x yz=4 x yz =6 multiplying 2nd Eq thru by 1 to eliminate both x and yLearning Objectives 421 Calculate the limit of a function of two variables;



Find The Absolute Maximum And Minimum Values Off On The Set D Math F X Y X 2 Y 2 2x Math D Is The Closed Triangular Region With Vertices 2 0 0



Tangent Plane To X 2 Xy Y 2 Z 0 Youtube
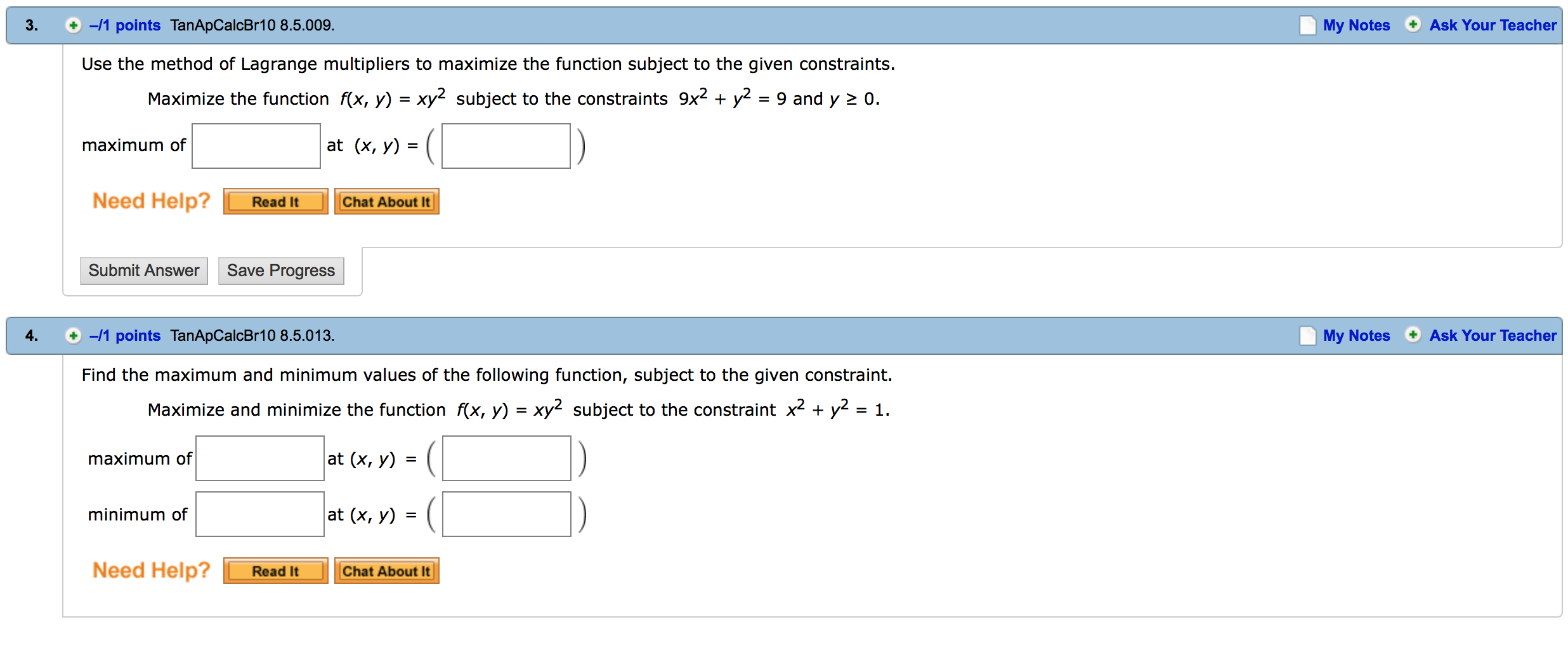
物理数学基礎演習演習問題 (平成29年度版) 1 偏微分 11 偏微分係数と偏導関数 問題11 次の2 変数関数z = f(x;y) の1 階偏導関数を求めよ. (1) z = x3 4x2y xy 3y2 (2) z = yX y z = 1 Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint (If a value does not exist, enter NONE) f(x,y,z) = x2 y2 z2;14) Objective function \(f(x, y, z) = x^2 y^2 z^2\) Constraint \(x^4y^4z^4=1\) 15) Objective function \(f(x, y, z) = x^2 y^2 z^2\) Constraint \(xyz=4\) In exercises 1621, use the method of Lagrange multipliers to find the requested extremum of the given function subject to the given constraint 16) Maximize \(f(x,y) = \sqrt{6 x



Solving A System Of Equations Using A Matrix Precalculus Socratic



Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5
X4 y4 z4 = 1 (maximum) (minimum) Assignment DetailsZ 4 1 Zp x x 2 Z x 0 (z xy) dzdydx (c) Z 2 0 Z y2 y2 Z x 0 (z xy) dzdxdy (d) Z 4 0 Zp x x 2 Z x 0 (z xy) dzdydx (e) Z y2 y Zp x x 2 Z xy 0 xdzdydx SolutionSolution The region Dis enclosed by the curves x= y2, x= y2, y= 0, and y= 2 The curve x= y2 is to the left and x= y2 is to the right Since the plane z= xlies above the xyplane forLet {eq}f(x,y,z)=x^2y^2z^2 {/eq} and let S be the level surface defined by f(x,y,z) = 4 (a) Find an equation for the plane tangent to S at {eq}P_{0}(1,1,2)



2x 3 Y 3z 5 X 2y Z 4 3x Y 2z 3 Youtube



Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1
Z 1 y 3 16 y 2 3 2 y 2 3 2 dy Z 1 1 3 y 16 y 2 3 2 y 4 dy 1 3 1 5 16 y 2 5 2 y from CALC 2302 at University of Texas, Dallas This preview shows page 56 59 out of pages
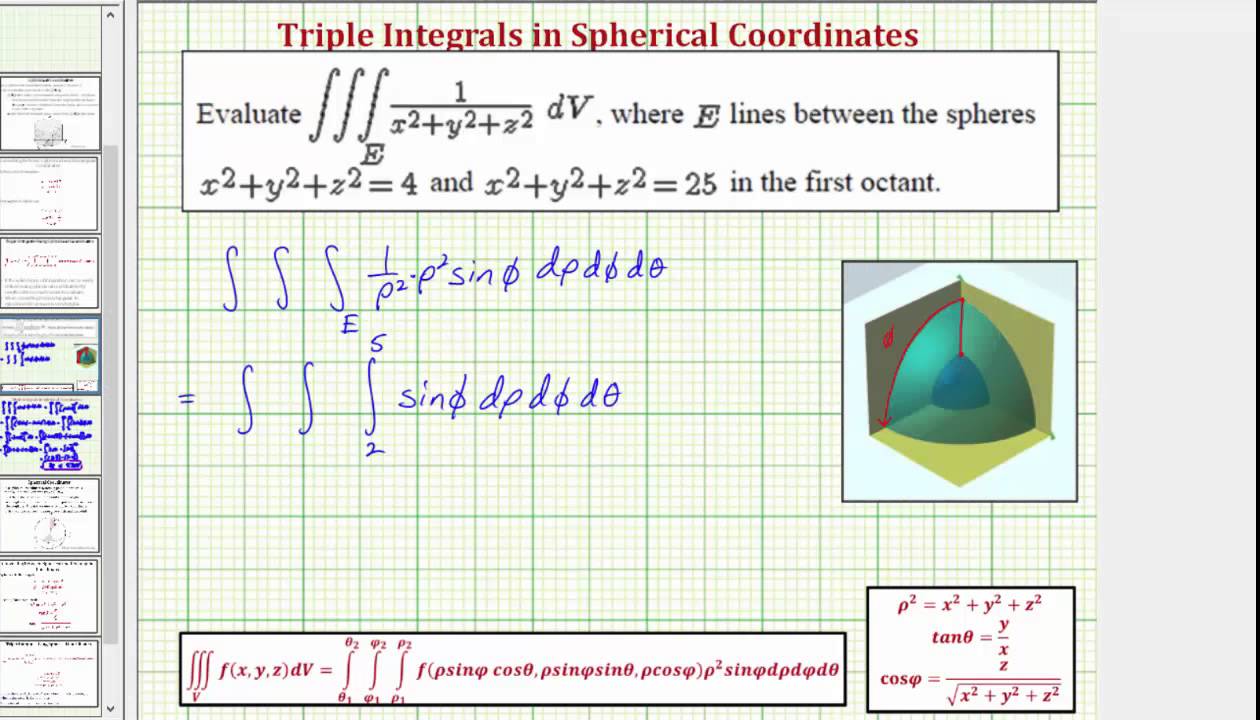


Evaluate A Triple Integral Using Spherical Coordinates Triple Integral Of 1 X 2 Y 2 Z 2 Youtube



Vector Analysis By Alimkanwalimtinaa Issuu



X Y Z 1 2x Y Z 2 X 2y Z 4 Youtube



Systems Engineering And Analysis Ppt Download



Use A Triple Integral To Find The Volume Of The Given Solid The Tetrahedron Enclosed By The Coordinate Planes And The Plane 2x Y Z 4 Homework Help And Answers Slader



Calc3 1001 By James Bardo Issuu
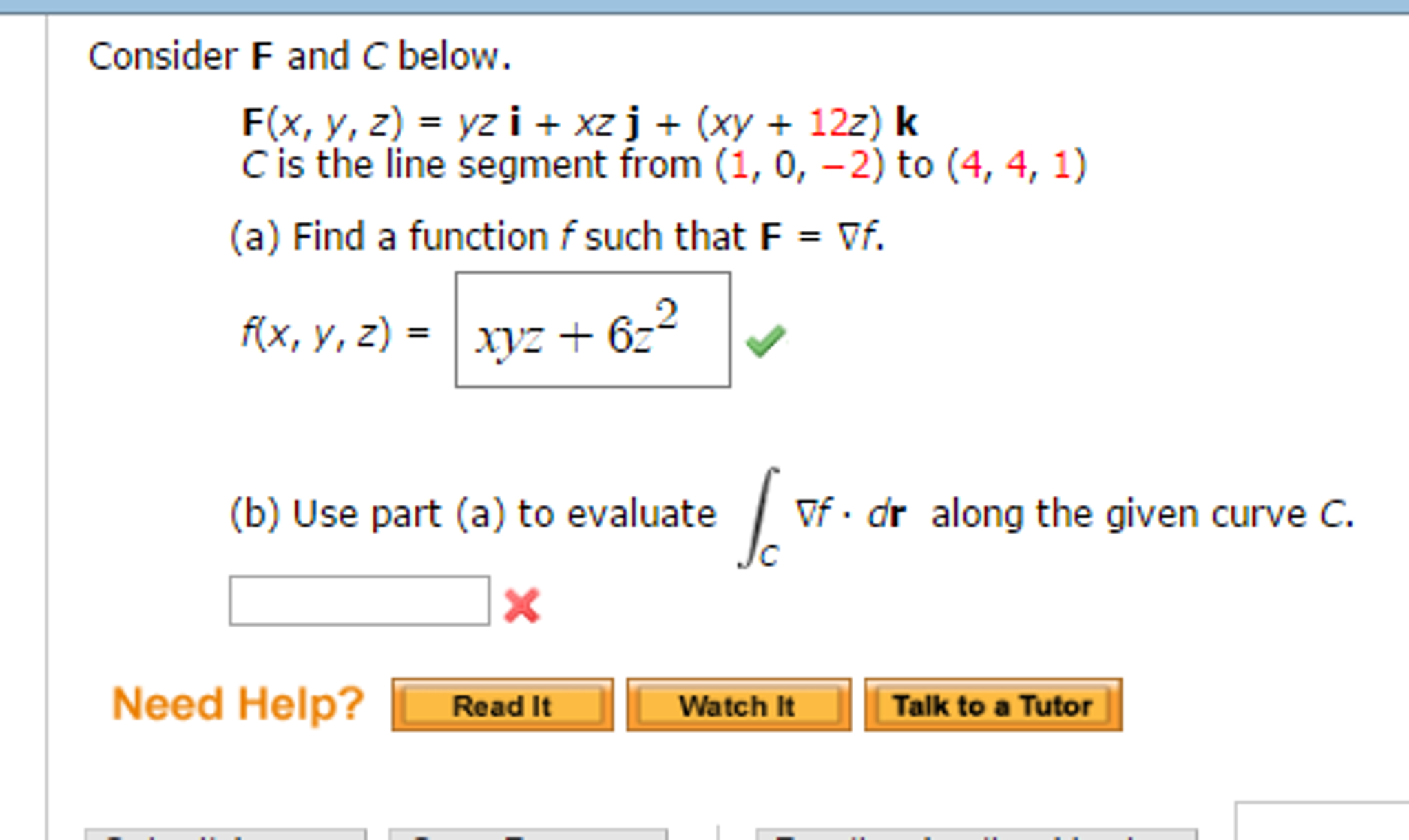


Solved Consider F And C Below F X Y Z Yz I Xz J Chegg Com



Solved Please Try And Answer All Of Them Show All Work Chegg Com



Assignment Previewer


How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic



Solutions To Homework Assignment 4 Math Pdf Free Download
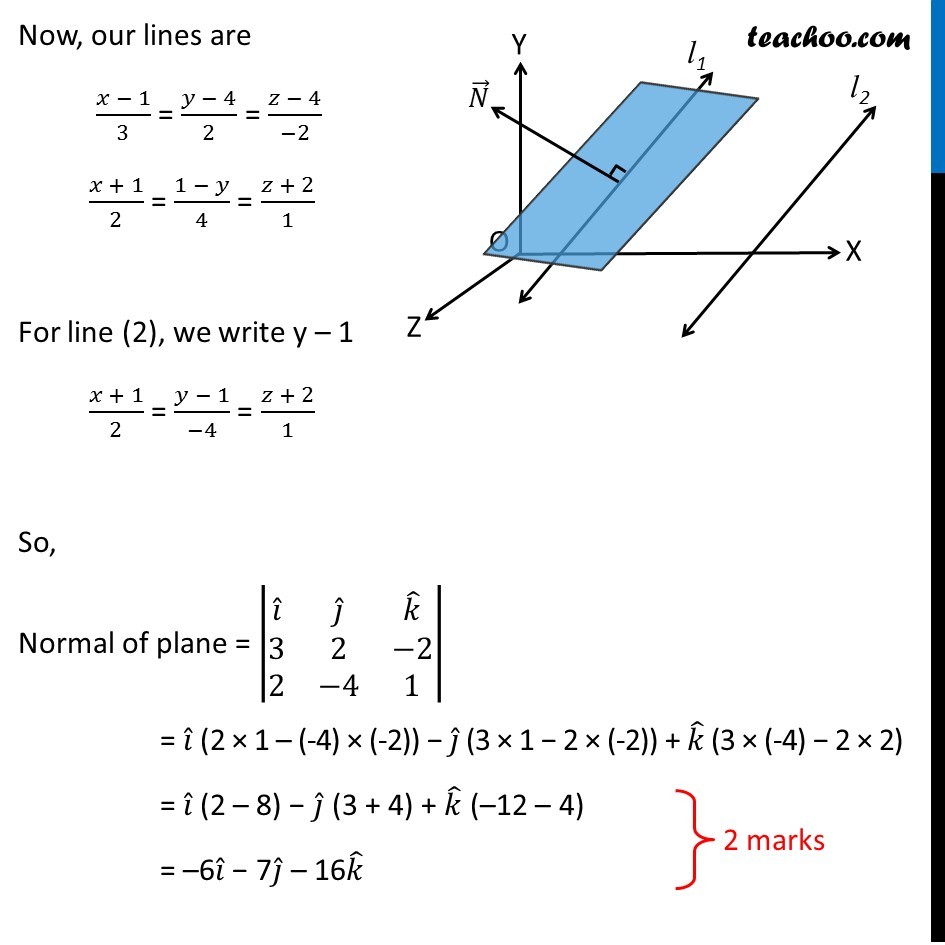


Find The Equation Of The Plane Through The Line X 1 3 Y 4 2



Solved Let F X Y Z 3x 2 5xy 2zy z 2 Be A Deg Chegg Com



X Y Xy 3 Y Z Yz 8 And Z X Zx 15 What Is The Value Of 6xyz Brainly In



Pde Tutorial Sheet



Solved Evaluate Partial Differential U Partial Differenti Chegg Com
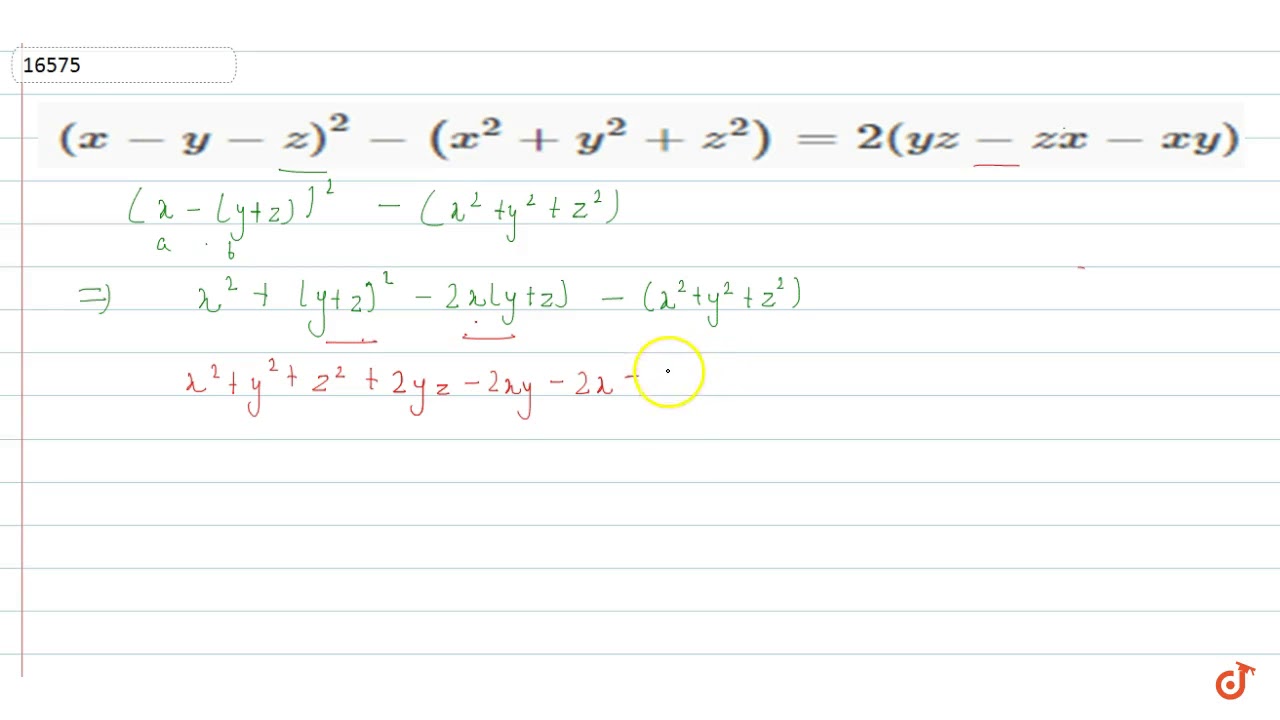


X Y Z 2 X 2 Y 2 Z 2 2 Yz Zx Xy Youtube



Analytical Geometry Notes



Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5



Solved This Extreme Value Problem Has A Solution With Bot Chegg Com



Solutions To Homework Assignment 4 Math Pdf Free Download


Solved Use The Method Of Lagrange Multipliers To Maximize Chegg Com



Vectors And The Geometry Of Space Monografias Com
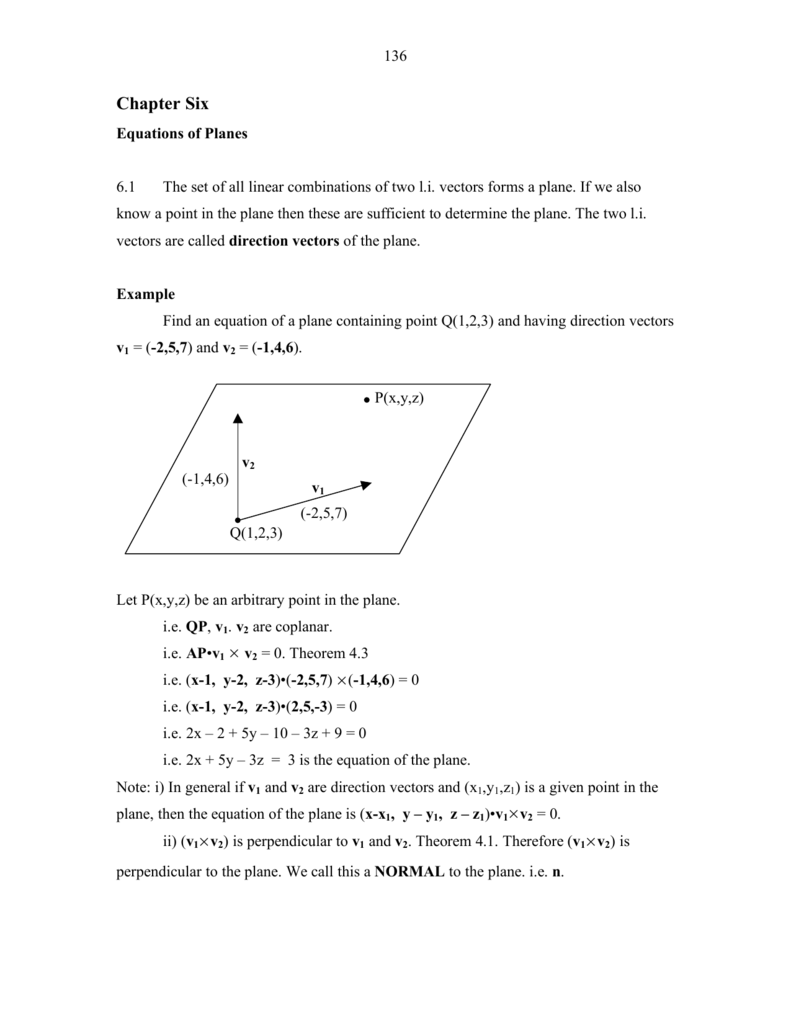


Chapter 6 Vectors Planes
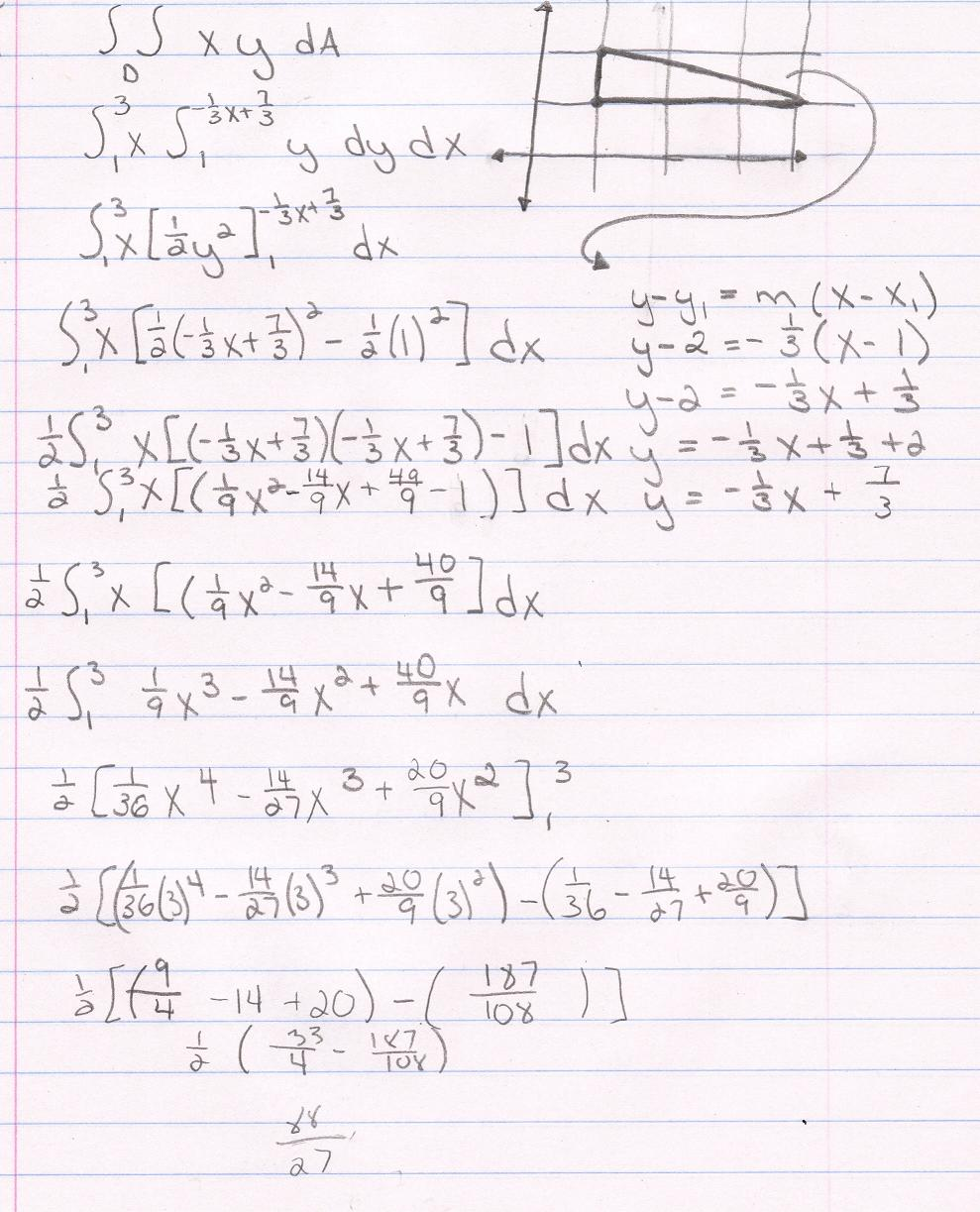


Solved Find The Volume Of The Given Solidunder The Surfac Chegg Com



Webwork Exam Review Solutions



Analytical Geometry Notes



Solved I Need Help With The Following Questions Really S Chegg Com



Using Cramer S Rule Solve 1 X 1 Y 1 Z 1 2 X 5 Y 3 Z 0 1 X 2 Y 4 Z 3 Youtube
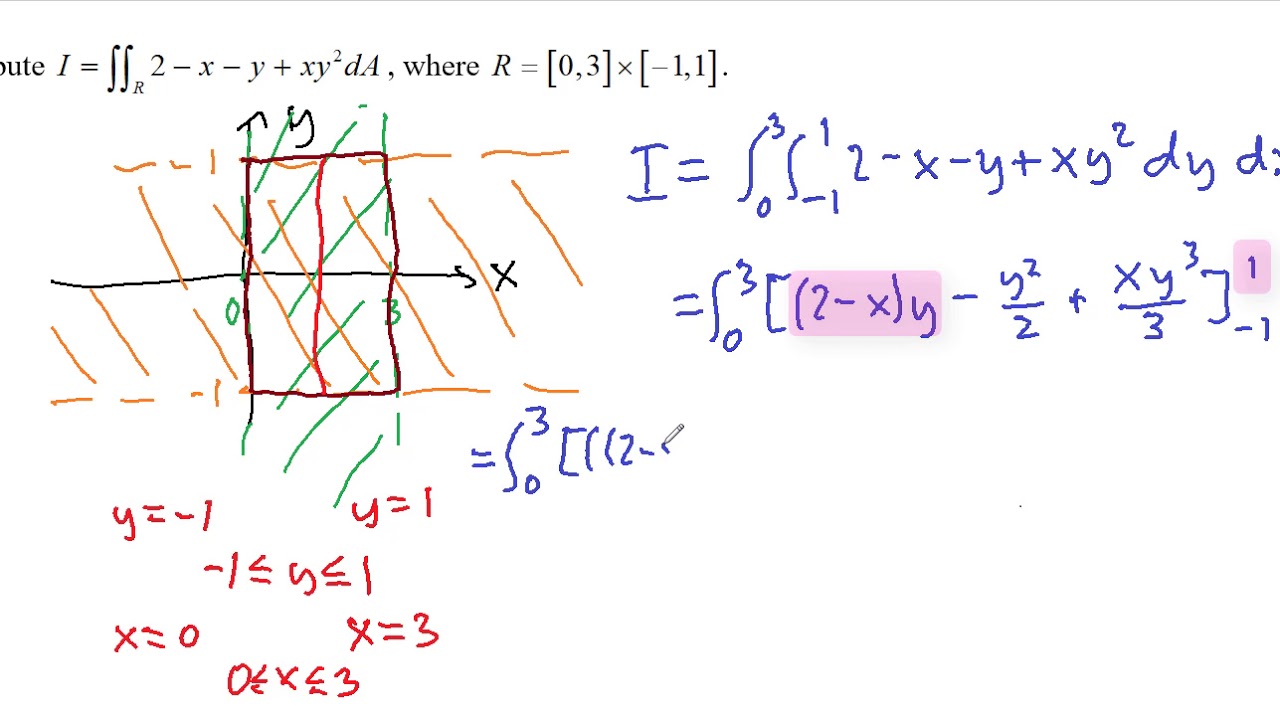


Double Integrals Volume And Average Value



Ex 3 2 12 Given 3 X Y Z W X 6 1 2w 4 X Y Z W 3



Chapter 16 1 16 3 Solutions Rogowski Pdf Document
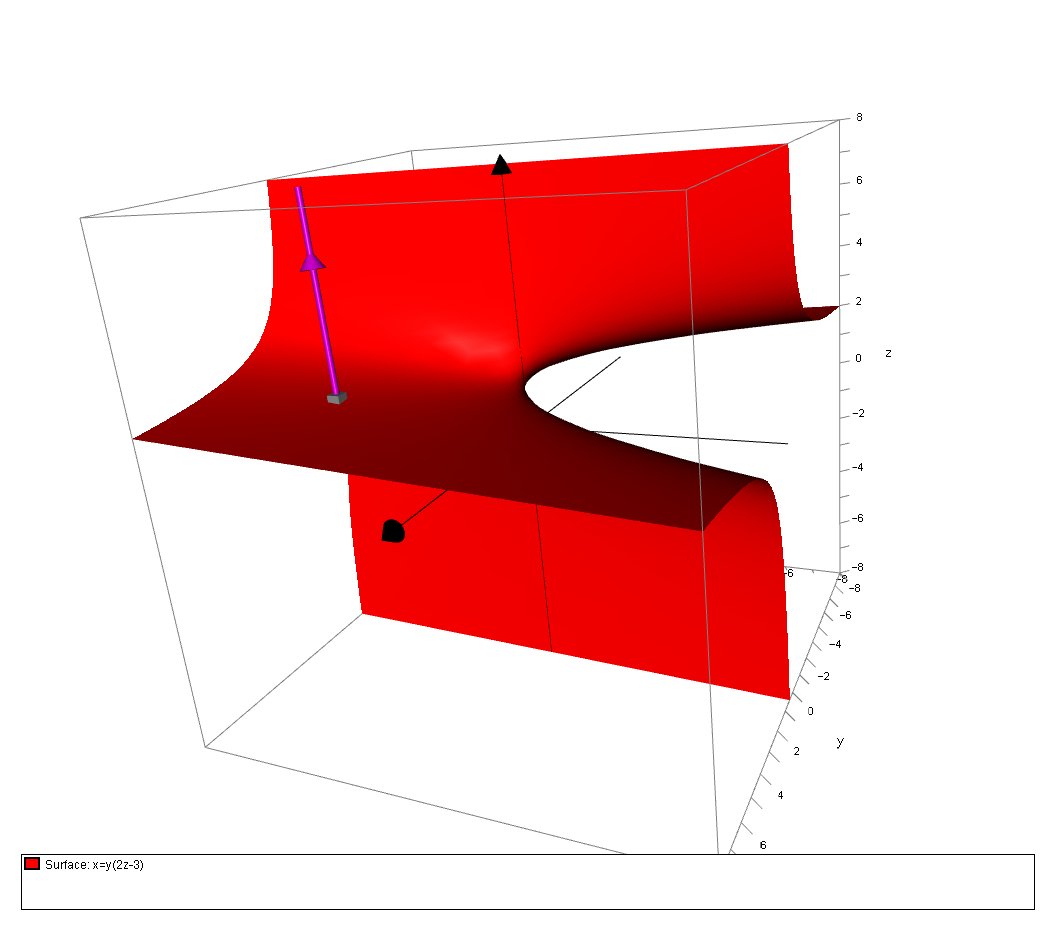


How Do You Find The Equations For The Tangent Plane To The Surface X Y 2z 3 Through 4 4 2 Socratic



Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy
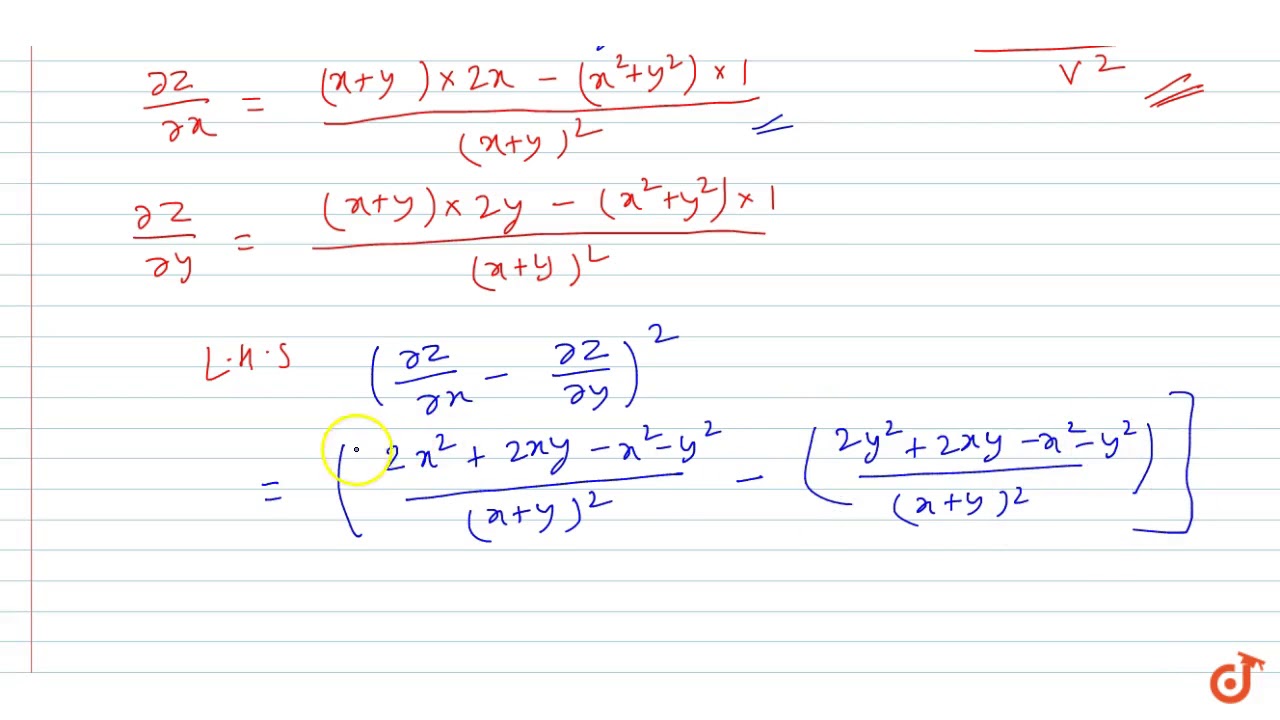


If Z X Y X 2 Y 2 Show That Delz Delx Delz Dely 2 4 1 Delz Delx Del Youtube



Find The Equation Of The Plane That Passes Through The Line Of Intersection Of The Planes Mathematics Stack Exchange



File



0 件のコメント:
コメントを投稿